LLM Core - Machine Learning Algorithm

线性回归

概述

1. 线性回归是一种预测分析技术，用于研究两个或者多个变量之间的关系
2. 尝试用一条直线（二维）或者一个平面（三维）的去拟合数据点
3. 这条直线或者平面，可以用来预测或者估计一个变量基于另一个变量的值

数学

1. 假设有一个因变量 y 和一个自变量 x
2. 线性回归会尝试找到一条直线 y=ax+b
   • a 为斜率，而 b 为截距
   • 以便这条直线尽可能地接近所有数据点

$$
y=ax+b
$$

sklearn

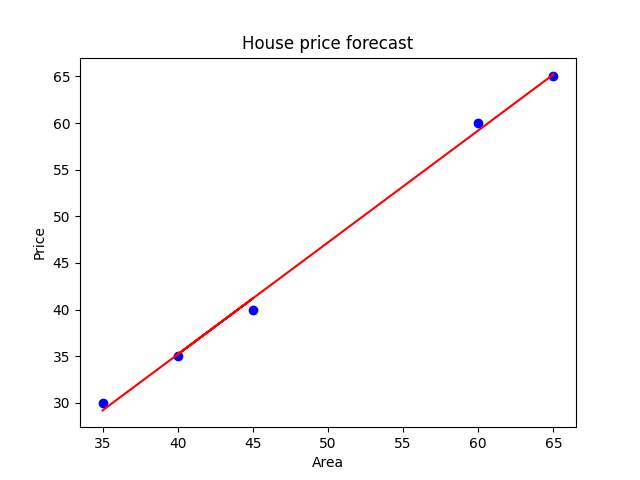
房价预测 - 房价是因变量 y，而房屋面积是自变量 x

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression

# 定义数据
X = np.array([35, 45, 40, 60, 65]).reshape(-1, 1)  # 面积
y = np.array([30, 40, 35, 60, 65])  # 价格

# 创建并拟合模型
model = LinearRegression()
model.fit(X, y)

# 预测面积为50平方米的房屋价格
predict_area = np.array([50]).reshape(-1, 1)
predicted_price = model.predict(predict_area)

print(f"预测的房价为：{predicted_price[0]:.2f}万美元")  # 预测的房价为：47.20万美元

# 绘制数据点和拟合直线
plt.scatter(X, y, color='blue')
plt.plot(X, model.predict(X), color='red')
plt.title('House price forecast')
plt.xlabel('Area')
plt.ylabel('Price')
plt.show()

1. 蓝色的点代表用于训练模型的实际数据点
2. 红色的线用于展示模型拟合的结果
3. 拟合 - 直线尝试穿过所有的数据点

逻辑回归

概述

1. 逻辑回归主要用于处理分类问题，尤其是二分类问题
2. 目的 - 预测一个事件的发生概率，并将这个概率转化为二元结果 - 0/1

数学

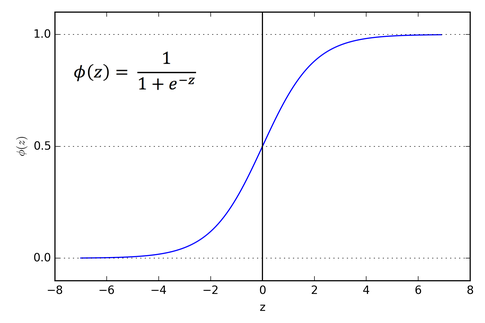
逻辑回归通过使用 Sigmoid 函数将线性回归模型的输出映射到 0 和 1 之间的概率值上

$$
\sigma(z)=\frac{1}{1+e^{-z}}
$$

1. $z$​ 为线性回归模型的输出
2. $z=\beta_{0}+\beta_{1}x_{1}+…+\beta_{n}x_{n}$，其中 $x_{n}$ 为特征变量，而 $\beta_{n}$ 为模型参数
3. 要取得模型参数的值，需要用到似然函数 - 基于观测，通过结果反推模型参数
4. 在某些特定场景下，得出了 $\sigma$，并且到了 $x_{n}$ 的值
   • 可以推测出使得 $\sigma$ 取得（准确率）最大的 $\beta_{n}$ 的值
   • 使用这个 $\beta_{n}$ 的值作为模型参数，从而进行概率推导

sklearn

基于学习时间，预测学生是否会通过考试，分为两类：通过为 1，未通过为 0

from sklearn.linear_model import LogisticRegression
import numpy as np

# 准备数据
X = np.array([[10], [20], [30], [40], [50]])  # 学习时间
y = np.array([0, 0, 1, 1, 1])  # 通过考试与否

# 创建逻辑回归模型并训练
model = LogisticRegression()
model.fit(X, y)

# 预测学习时间为25小时的学生通过考试的概率
prediction_probability = model.predict_proba([[25]])
prediction = model.predict([[25]])
print(f"通过考试的概率为：{prediction_probability[0][1]:.2f}")  # 通过考试的概率为：0.50
print(f"预测分类：{'通过' if prediction[0] == 1 else '未通过'}")  # 预测分类：通过

决策树

概述

1. 决策树主要用于分类和回归任务
2. 从数据中学习决策规则来预测目标变量的值
3. 场景 - 猜谜游戏 - 客户分类 / 信用评分 / 医疗诊断
   • 每次只能问 1 个问题，对方只能回答是或否
   • 目标 - 用最少的问题才出答案 - 高效决策

sklearn

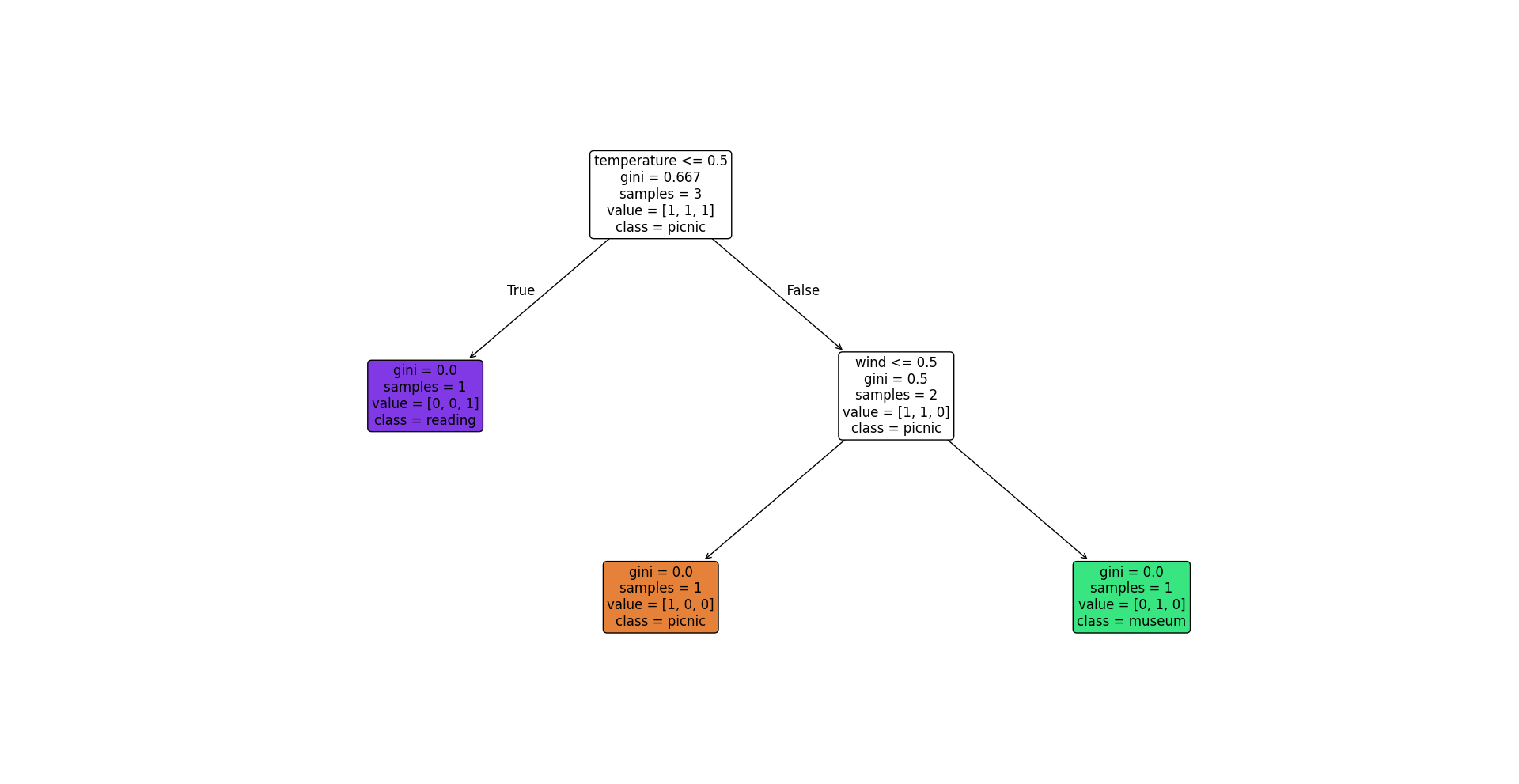
根据天气情况、温度和风速来决定进行什么活动

from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
import numpy as np

# 创建数据集
X = np.array([
    [0, 2, 0],  # 晴天，高温，无风
    [1, 1, 1],  # 阴天，中温，微风
    [2, 0, 2],  # 雨天，低温，强风
    # ... 添加更多样本以增加模型的准确性
])
y = np.array([0, 1, 2])  # 分别对应去野餐、去博物馆、在家看书

# 初始化决策树模型，设置最大深度为5
clf = DecisionTreeClassifier(max_depth=5, random_state=42)

# 训练模型
clf.fit(X, y)

# 可视化决策树
plt.figure(figsize=(20, 10))
plot_tree(clf, filled=True,
          feature_names=["weather", "temperature", "wind"],  # 分别对应天气、温度、风力
          class_names=["picnic", "museum", "reading"],
          rounded=True, fontsize=12)
plt.show()

指标

1. gini 指数 - 纯度
   • 衡量节点纯度的指标，用于分类问题
   • 一个节点的 gini 指数越低，表示这个节点包含的样本越倾向于同一个类别
   • 0 表示所有样本都属于同一类别，即完全纯净
2. samples - 样本总数
   • 表示到达这个节点的样本数量
   • 提供了关于树的分支如何基于数据集进行分割的直观理解
   • 可以用于帮助评估决策树各个部分的数据覆盖范围
3. value - 样本分布
   • 表示这个节点每个类别的样本数量
   • 该数组提供了分类分布的具体信息
   • 有助于了解每个决策节点处数据是如何被分割的
4. class - 主要类别/预测类别
   • 代表在当前节点样本中占多数的类别
   • 如果一个节点是叶子节点，那么该类别就是这个节点的预测类别
   • 如果一个节点是非叶子节点，那么该类别就是这个节点的主要类别

作用

1. 可以理解决策树是如何根据特征分割数据
2. 还可以评估树的深度、每个节点的决策质量、模型是否可能出现过拟合
   • 过拟合 - 某些叶子节点上只有很少的样本
3. 指标是调整模型参数来优化模型性能的重要依据
   • 树的最大深度
   • 进行节点分割的最少样本数

随机森林

概述

1. 随机森林属于集成学习家族
2. 随机森林可以通过构建多个决策树来进行预测
3. 基本思想 - 集体智慧 - 多个模型集合起来可以作出更好的判断
4. 随机森林的关键 - 随机性

随机性	描述
样本随机性	每棵树训练的数据通过从原始数据中进行随机抽样得到 - 自助采样
特征随机性	在分裂决策树节点时，从所有特征中随机选取一部分特征 然后只在这些随机选取的特征中寻找最优分裂特征

随机森林的随机性，使得模型具有很高的准确性，同时能防止模型过拟合
过拟合 - 因为训练数据或者模型参数导致模型缺乏泛化能力

1. 泛化能力 ≈ 通用能力
2. 训练模型的目的是希望模型解决通用问题
3. 场景 - 训练一个模型，用来识别一个照片中有没有狗
   • 训练完成后，只能识别直尾巴的狗，因为有一个参数是描述尾巴是直的还是弯的
   • 该参数的存在使得模型额外识别了狗的另一个（不重要的）特征，失去了泛化能力 - 过拟合

决策树

决策树会出现过拟合 - 不通用，缺少泛化能力

1. 如果一个决策条件中有一个非常不通用的条件，分类后的分支节点只有一个样本
2. 说明该决策没有通用性（缺少泛化能力），那么这个决策树模型存在过拟合的问题

工作原理

随机森林可以解决决策树过拟合的问题

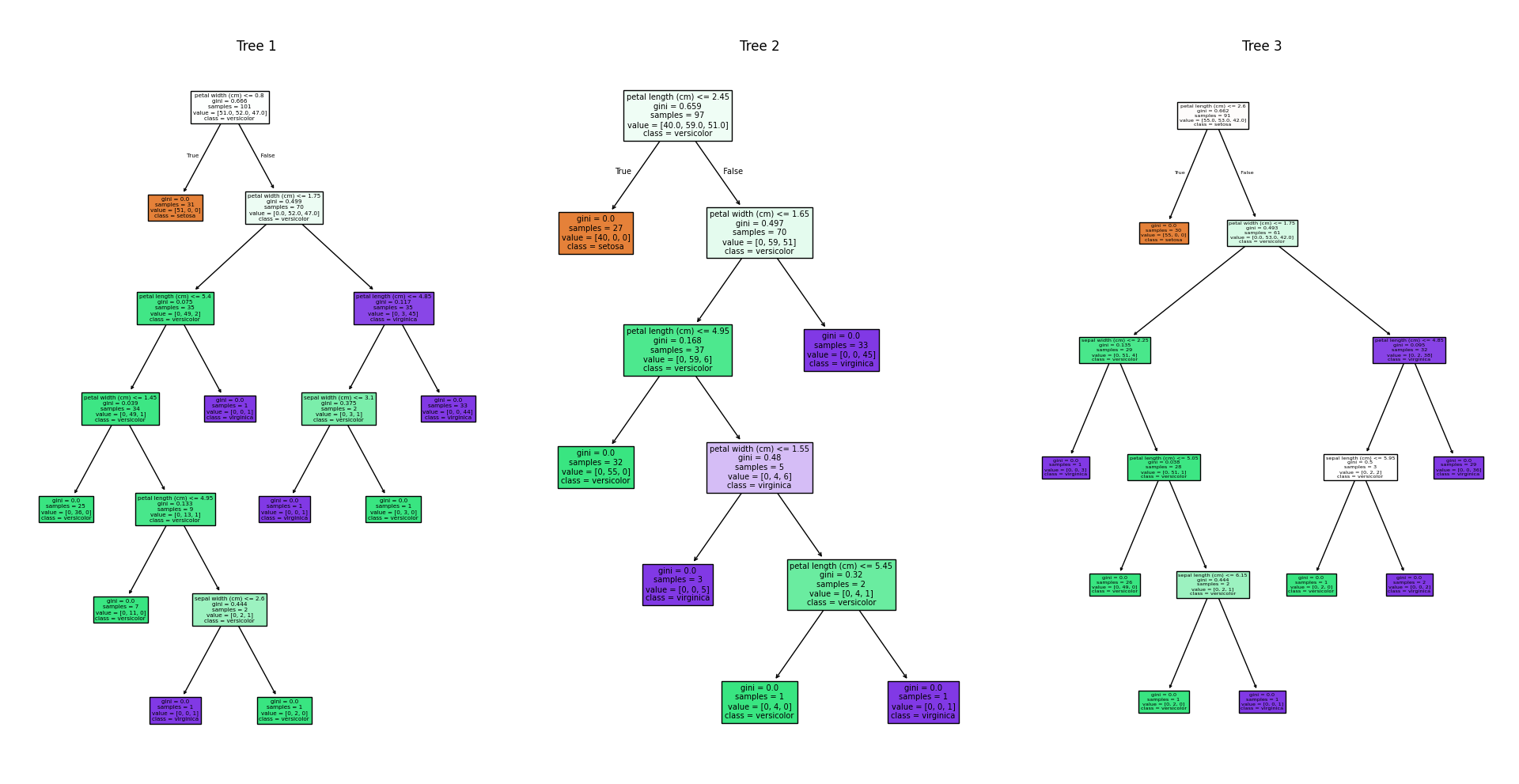
1. 训练 - 随机
   • 从原始数据集中随机抽样选取多个子集
   • 每个子集训练一个决策树
2. 决策 - 独立 + 投票
   • 每棵树独立进行预测
   • 最终预测结果是所有的树预测结果的投票或者平均

sklearn

import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris

# 加载数据集
# The iris dataset is a classic and very easy multi-class classification dataset.
iris = load_iris()
X, y = iris.data, iris.target

# 训练随机森林模型
rf = RandomForestClassifier(n_estimators=3, random_state=42)  # 使用3棵树以便于可视化
rf.fit(X, y)

# 绘制随机森林中的决策树
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(20, 5), dpi=100)
for index in range(0, 3):
    plot_tree(rf.estimators_[index],
              feature_names=iris.feature_names,
              class_names=iris.target_names,
              filled=True,
              ax=axes[index])

    axes[index].set_title(f'Tree {index + 1}')

plt.tight_layout()
plt.show()

决策步骤

步骤	操作
独立预测	对于每个输入样本，随机森林中的每棵树都会独立作出预测
投票计数	收集到所有树对每个样本的预测结果，并对这些结果进行计数
决定决策	对于每个样本，被预测次数最多的类别将成为随机深林的最终预测结果

在实际应用中，可以构造更多的决策树来进行预测，使得模型更准确更稳定

支持向量机

Support Vector Machine - SVM

概述

寻找不同类别间的很粗且清晰的界线，该界线由距离最近的几个点（支持向量）决定

优势

1. 在分类决策时，不仅仅依赖数据的分布
2. 并且具有很好的泛化能力，能够应对未见过的新数据

核心思想

1. 支持向量机是一种强大的分类算法，在数据科学和机器学习领域广泛应用
2. 核心思想
   • 找到一个最优的决策边界 - 即超平面
   • 超平面能够以最大的间隔将不同类别的数据分开

超平面

1. 在二维空间中，边界为一条线

2. 在三维空间中，边界为一个平面

3. 在高维空间中，边界为超平面

4. 边界的目的 - 尽可能准确地分隔开不同类别的数据点

最大间隔

1. SVM 寻找的是能够以最大间隔分开数据的边界
2. 间隔 - 是不同类别中的数据点到这个边界的最小距离
3. SVM 试图使得该最小距离尽可能大
4. 目的 - 更能抵抗数据中的小变动，提高模型的泛化能力

支持向量

1. 支持向量 - 决定最优超平面位置的几个关键数据点
2. 这些关键数据点不同类别中是最靠近决策边界的数据点
3. 最大间隔的边界就是通过这些关键数据点来确定的

核技巧

升维 -> 线性可分

1. 当数据不是线性可分时 - 即无法通过一条直线或者一个平面来分隔

2. SVM 可以利用核技巧将数据映射到一个更高维的空间 - 数据可能会线性可分

3. 核技巧使得 SVM 在处理非线性数据时非常强大

sklearn

from sklearn import datasets
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np

# 生成模拟数据
X, y = datasets.make_blobs(n_samples=50, centers=2, random_state=6)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建 SVM 模型
model = SVC(kernel='linear')  # 线性核
model.fit(X_train, y_train)

# 绘制数据点和分类边界
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

# 绘制决策边界
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

# 创建网格点
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)

# 绘制决策边界和间隔
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
plt.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100, linewidth=1, facecolors='none',
            edgecolors='k')
plt.title("SVM Classification")
plt.xlabel("Feature A")
plt.ylabel("Feature B")
plt.show()

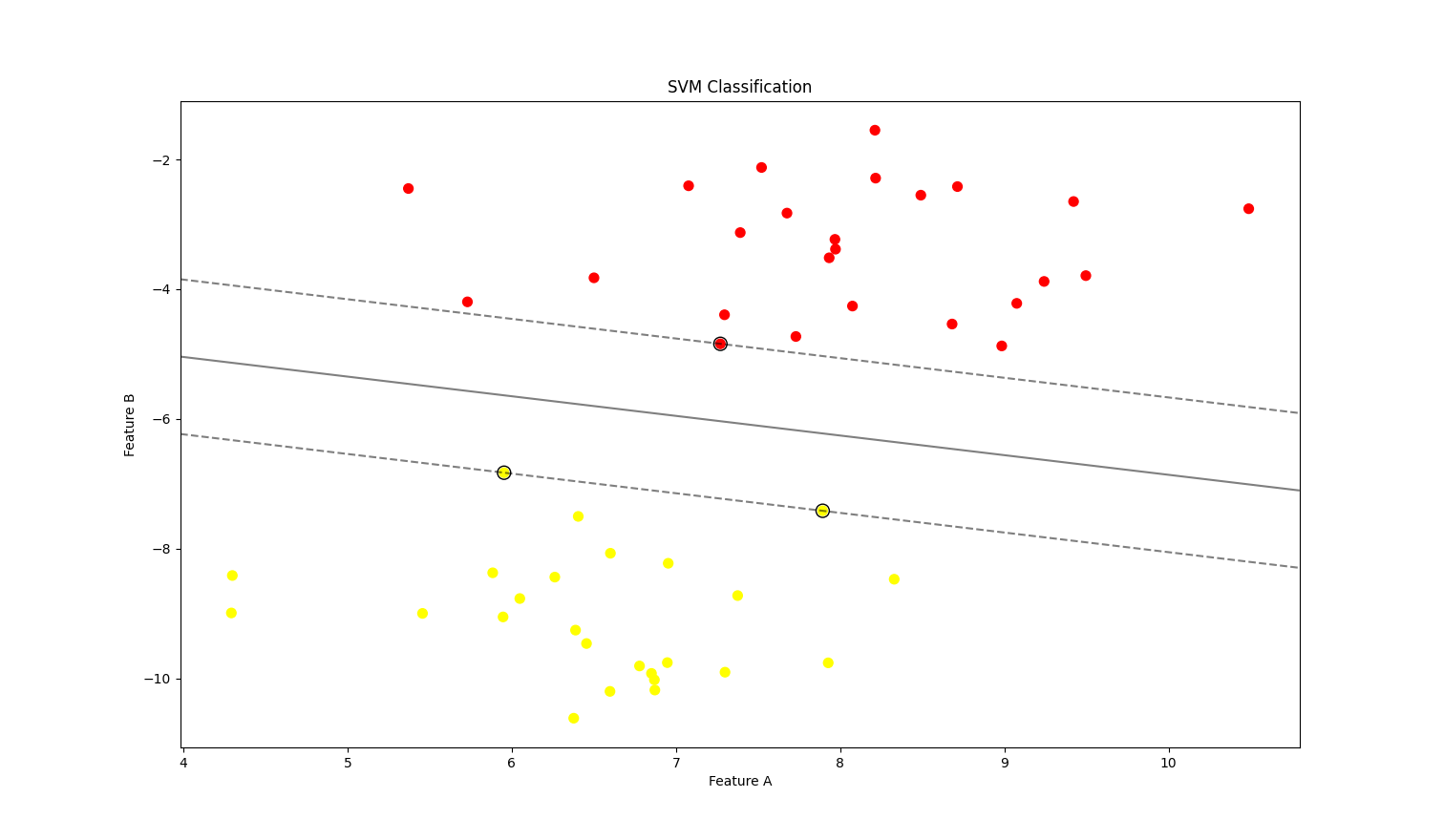
1. 使用线性核的 SVM 模型来分类模拟生成的数据点 - 橙色和黄色代表不同的类别
2. 黑色实线 - 决策边界 - 即 SVM 找到的最优超平面 - 用于将两类数据分开
3. 虚线 - 决策边界的边缘 - 最大间隔的边界 - 这些边缘之间的区域就是模型的间隔
4. 黑色圆圈 - 支持向量 - 不同类别中离决策边界最近的几个点 - 用于确定决策边界

核函数 - 升维 - 线性可分

1. 上述例子可以通过直线完成分类 - 线性可分 - 无需升维
2. 如果数据无法通过直线进行分类，则需要进行升维
   • 在三维空间，通过一个平面进行分类
3. SVM 可以选择不同的核函数来处理更复杂的数据集

神经网络

概述

1. 现在大部分的主流 LLM 都是基于深度神经网络
2. 设计思路
   • 模仿大脑，由许多小的、处理信息的单位组成 - 神经元
   • 各个神经元之间彼此连接，每个神经元可以向其它神经元发送和接收信号
3. 神经网络能够执行各种复杂的计算任务 - 图像识别 / 语音识别 / 自然语言处理等

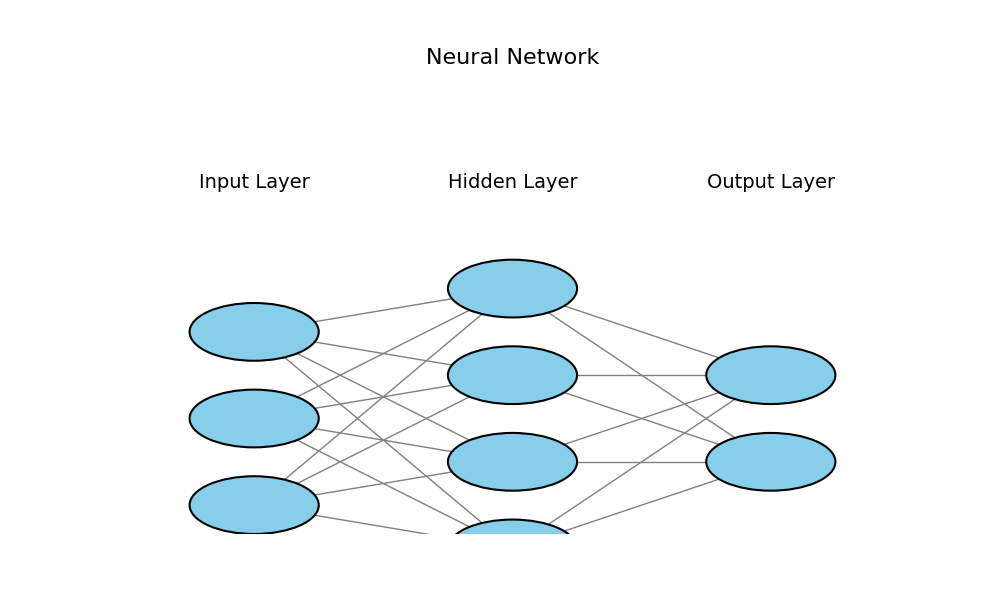
结构

输入层 + 隐藏层（多层） + 输出层

Layer	Desc
输入层	接收原始数据输入 - 图片的像素值 / 一段文本的编码
隐藏层	处理输入数据，可以有一个或多个隐藏层 隐藏层的神经元会对输入数据进行加权和，应用激活函数 可以捕捉输入数据中的复杂模式和关系
输出层	根据隐藏层的处理结果，输出一个值或者一组值 - 最终预测结果

优势

非线性 -> 处理复杂任务

1. 神经网络是非线性的，可以理解非常复杂的逻辑关系
2. 在深层神经网络中，不同的层可以学习到不同的特征
   • 较低的层可能学习简单的特征
   • 较高的层可以学习到更复杂的概念
3. 从简单到复杂的学习过程使得神经网络非常适合处理复杂的数据结构

组件

Component	Desc
激活函数	赋予不同的特性
前向传播	逐层处理输入数据，通过各种操作和激活函数的作用 逐渐提取并组合数据的特征，最终得到输出结果
训练过程	通过反向传播算法来调整网络参数 使得网络的输出尽可能接近真实标签，达到最佳预测效果
反向传播	通过计算模型输出与真实标签之间的差距（损失函数） 并利用链式法则逆向传播这个误差，调整每一层的参数，使得网络的输出更接近真实标签
梯度下降	是一种优化算法，通过不断沿着梯度的反方向调整参数 逐步降低损失函数，使得网络的预测效果逐渐提升，达到最优的训练效果
损失函数	衡量模型输出与真实标签之间差距，即模型的预测效果 损失函数越小表示模型的预测越接近真实标签

sklearn

import matplotlib.pyplot as plt


# 创建一个简单的神经网络图，并调整文字标签的位置
def plot_neural_network_adjusted():
    fig, ax = plt.subplots(figsize=(10, 6))  # 创建绘图对象

    # 输入层、隐藏层、输出层的神经元数量
    input_neurons = 3
    hidden_neurons = 4
    output_neurons = 2

    # 绘制神经元
    layer_names = ['Input Layer', 'Hidden Layer', 'Output Layer']
    for layer, neurons in enumerate([input_neurons, hidden_neurons, output_neurons]):
        for neuron in range(neurons):
            circle = plt.Circle((layer * 2, neuron * 1.5 - neurons * 0.75 + 0.75), 0.5, color='skyblue', ec='black',
                                lw=1.5, zorder=4)
            ax.add_artist(circle)

    # 绘制连接线
    for input_neuron in range(input_neurons):
        for hidden_neuron in range(hidden_neurons):
            line = plt.Line2D([0 * 2, 1 * 2], [input_neuron * 1.5 - input_neurons * 0.75 + 0.75,
                                               hidden_neuron * 1.5 - hidden_neurons * 0.75 + 0.75], c='gray', lw=1,
                              zorder=1)
            ax.add_artist(line)
    for hidden_neuron in range(hidden_neurons):
        for output_neuron in range(output_neurons):
            line = plt.Line2D([1 * 2, 2 * 2], [hidden_neuron * 1.5 - hidden_neurons * 0.75 + 0.75,
                                               output_neuron * 1.5 - output_neurons * 0.75 + 0.75], c='gray', lw=1,
                              zorder=1)
            ax.add_artist(line)

    # 设置图参数
    ax.set_xlim(-1, 5)
    ax.set_ylim(-2, max(input_neurons, hidden_neurons, output_neurons) * 1.5)
    plt.axis('off')  # 不显示坐标轴

    # 调整层名称的绘制位置，确保不被遮挡
    for i, name in enumerate(layer_names):
        plt.text(i * 2, max(input_neurons, hidden_neurons, output_neurons) * 0.75 + 1, name,
                 horizontalalignment='center', fontsize=14, zorder=5)

    plt.title("Neural Network", fontsize=16)
    return fig


fig = plot_neural_network_adjusted()
plt.show()