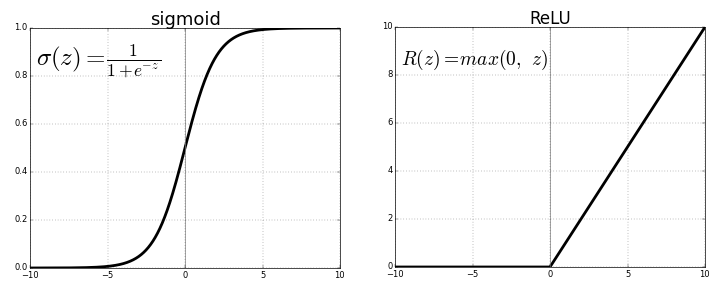LLM Core - RNN
背景
- RNN 主要用来处理序列数据,目前大部分 LLM 都是基于 Transformer
- 通过学习 RNN,有助于理解 Transformer
- 有助于理解神经网络如何处理序列中的依赖关系、记忆过去的信息,并在此基础上生成预测
- 有助于理解关键问题 - 梯度消失 / 梯度爆炸
RNN
Recurrent neural network - 循环神经网络
- RNN 是一类用于处理序列数据的神经网络,RNN 能够处理序列长度变化的数据 - 文本 / 语音
- RNN 的特点是在模型中引入了循环,使得网络能够保持某种状态,表现出更好的性能
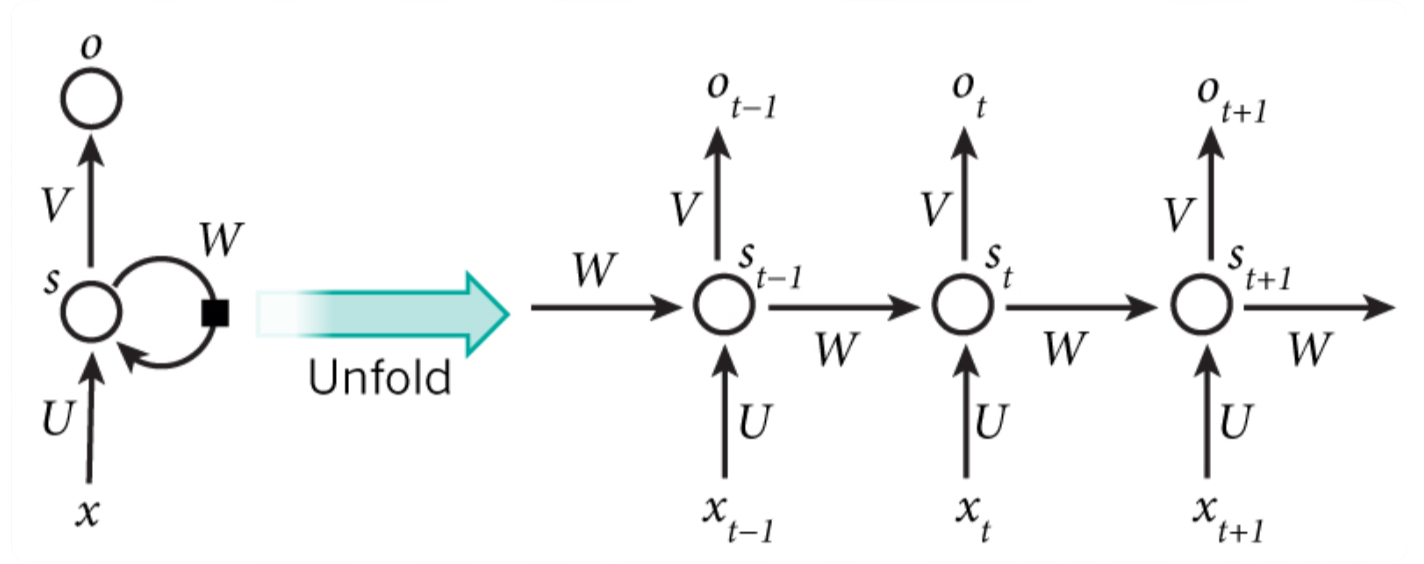
- 左边
- $x$ 为输入层,$o$ 为输出层,中间的 $s$ 为隐藏层,在 $s$ 层进行一个循环 $W$
- 右边(展开循环)
- 与时间 $t$ 相关的状态变化
- 神经网络在处理数据时,能看到前后时刻的状态,即上下文
- RNN 因为隐藏层有时序状态,那么在推理的时候,可以借助上下文,从而理解语义更加准确
优劣
优势
- RNN 具有记忆能力,通过隐藏层的循环结构来捕捉序列的长期依赖关系
- 特别适用于文本生成、语音识别等领域
局限
- 存在梯度消失和梯度爆炸的问题,可以通过引入 LSTM 来缓解
反向传播
- 在深度学习中,训练神经网络涉及到两个主要的传播阶段 - 前向传播 + 反向传播
- 前向传播 - 根据当前的网络参数、权重和偏置等得到预测输出
- 输入数据从网络的输入层开始,逐层向前传递至输出层
- 每层都会对其输入进行计算 - 如加权求和,然后应用激活函数等
- 并将计算结果传递给下一层,直到最终产生输出
- 反向传播
- 一旦输出层得到了预测输出,就会**计算损失函数**
- 即预测输出与实际目标输出之间的差异(损失)
- 然后,这个损失会被用来计算损失函数相对于网络中每个参数的梯度
- 这些梯度的内涵 - 为了减少损失,各个参数需要如何调整
- 链式法则 - 从输出层开始,沿着网络向后(向输入层方向),逐层进行
- 最后这些梯度会用来更新网络的参数 - 通过梯度下降或者其变体算法实现
- 在反向传播过程中,每到达一层,都会触发激活函数
- tanh 函数可能会导致梯度消失
- 一旦输出层得到了预测输出,就会**计算损失函数**
结构原理
数学
RNN 的核心在于隐藏层 - 随着时间的变化更新隐藏状态
$$
h_t=f(W_{xh}x_t+W_{hh}x_{t-1}+b_h)
$$
- $h_t$ 是当前时间步的隐藏状态,$x_t$ 是当前时间步的输入,$h_{t-1}$ 是前一个时间步的隐藏状态
- $W_{xh}$ 和 $W_{hh}$ 为权重矩阵,$b_h$ 是偏置项,$f$ 是激活函数(如 tanh 函数)
过程
任务 - 假设字符集只有 A B C,给定序列 AB,预测下一个字符
- 在输入层,将字符串转换为数值形式 - Embedding
- 可以采用 One-hot 编码,A=[1,0,0] B=[0,1,0] C=[0,0,1]
- 序列 AB,表示为两个向量 [1,0,0] 和 [0,1,0]
- 在隐藏层,假设只有一个隐藏层(实际应用可能会有多个),使用 tanh 作为激活函数
- 时间步 1 - 处理 A
- 输入 [1,0,0]
- 假设 $W_{xh}$ 和 $W_{hh}$ 的值均为 1,初始隐藏状态 $h_0=0$
- 计算新的隐藏状态 $h_1=tanh(1*[1,0,0]+1*0)=tanh(1)≈0.76$
- 时间步 2 - 处理 B
- 输入 [0,1,0]
- 使用上一时间步的隐藏状态 $h_1≈0.76$
- 计算新的隐藏状态 $h_2=tanh(1*[0,1,0]+1*0.76)=tanh(0.76)≈0.64$
- 时间步 1 - 处理 A
每个时间步的隐藏状态 $h_t$ 基于当前的输入 $x_t$ 和上一时间步的隐藏状态 $h_{t-1}$ 计算得到的
RNN 能够记住之前的输入,并使用这些信息影响后续的处理,如预测下一个字符,使得模型具备了记忆功能
One-hot
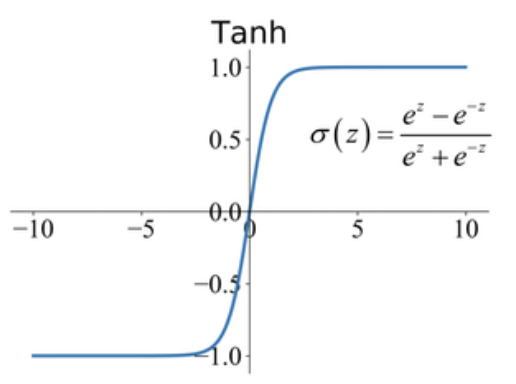
tanh
压缩器
关键挑战
- RNN 通过当前的隐藏状态来记住序列之前的信息
- 这种记忆一般是短期的,随着时间步的增加,早期输入对当前状态的影响会逐步减弱
- 在标准 RNN 中,可能会遇到梯度消失的问题,导致几乎无法更新权重
| 挑战 | 影响 |
|---|---|
| 梯度消失 | 权重无法更新 |
| 梯度爆炸 | 无法收敛,甚至发散 |
梯度消失
无法更新权重
概述
- 梯度是指函数在某一点上的斜率 - 导数
- 在深度学习中,该函数一般指具有多个变量(模型参数)的损失函数
- 寻找损失函数最小值的方法 - 梯度下降
- 梯度下降 - 需要不断调整模型参数,使得损失函数降到最小
- 梯度的语义 - 告知如何调整参数
原因
深层网络中的连乘效应
在深层网络中,梯度是通过链式法则进行反向传播的
如果每一层的梯度都小于 1,随着层数的叠加,导致最终的梯度会非常小
激活函数的选择 - 反向传播会调用激活函数
使用某些激活函数,如 tanh,函数的取值范围在 -1 ~ 1
小于 1 的数进行连乘,会快速降低梯度值
方案
长短期记忆(LSTM)和门控循环单元(GRU) - 专门为了避免梯度消失问题而设计
通过引入门控机制来调节信息的流动,保留长期依赖信息
从而避免梯度在反向传播过程中消失
使用 ReLU 及其变体激活函数 - 在正区间的梯度保持恒定
- 不会随着输入的增加而减少到 0,有助于减轻梯度消失的问题
ReLU 函数
梯度爆炸
模型无法收敛,甚至发散
概述
- 当模型的梯度在反向传播过程中变得非常大
- 以至于更新后的权重**偏离最优解,导致模型无法收敛,甚至发散**
原因
深层网络的连乘效应
在深层网络中,梯度是通过链式法则进行反向传播的
如果每一层的梯度都大于 1,随着层数的增加,会导致梯度非常大
权重初始化不当
如果网络的权重初始化得太大
在前向传播的过程中,信号大小会迅速增加
同样,反向传播时梯度也会迅速增加
使用不恰当的激活函数
某些激活函数(如 ReLU)在正区间的梯度为常数
如果网络架构设计不当,使用这些激活函数也可能会导致梯度爆炸
方案
- 使用长短期记忆(LSTM)和门控循环单元(GRU)来调整网络
- 替换激活函数
- 进行梯度裁剪
- 在训练过程中,通过限制梯度的最小最大值来防止梯度消失爆炸问题,间接保持梯度的稳定性
长短期记忆
Long Short-Term Memory - LSTM - 记住该记住的,忘记该忘记的 - 优化记忆的效率
概述
- LSTM 是具有类似大脑记忆功能的模块
- LSTM 在处理数据(如文本、时间序列数据时) - 能记住对当前任务重要的信息,而忘记不重要的信息
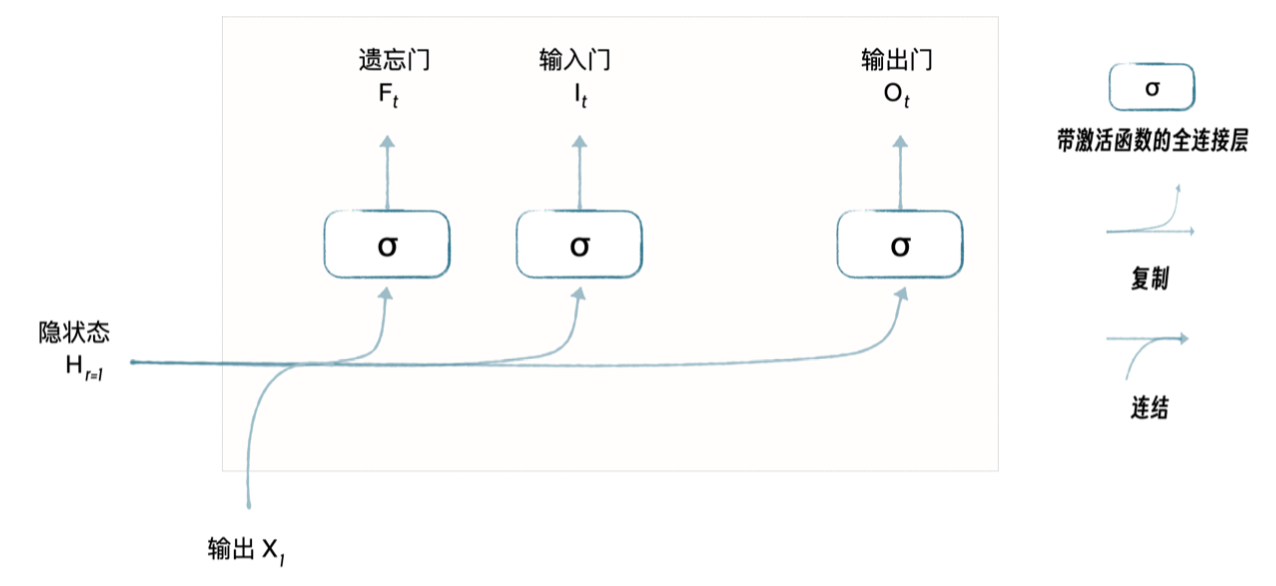
机制
| Mechanism | 描述 |
|---|---|
| 遗忘门 - 移除 | 决定哪些存量信息是过时的,不重要的,应该从模型的记忆中移除 |
| 输入门 - 添加 | 决定哪些新信息是重要的,应该被添加到模型的记忆中 |
| 输出门 - 相关 | 决定在当前时刻,哪些记忆是相关的,应该要被用来生成输出 |
效果
- LSTM 能够在处理序列数据时,**有效地保留长期的依赖信息,避免了标准 RNN** 中常见的梯度消失问题
- LSTM 特别适用于需要理解整个序列背景的任务
- 语言翻译 - 需要理解整个句子的含义
- 股票价格预测 - 需要考虑长期的价格变化趋势
文本生产
通过学习大量的文本数据,RNN 能够生成具有相似风格的文本
1 | import torch |